Improving Minimax Group Fairness in Sequential Recommendation

Table of Contents

📌

TL;DR: Training sequential recommenders like SASRec with uniform sample weights yields state-of-the-art overall metrics but can underperform for specific user groups. We explore three distributionally robust methods—Group DRO, Streaming DRO, and CVaR DRO—alongside traditional baselines such as Empirical Risk Minimization (ERM), inverse propensity weighting, and class-balanced loss.

CVaR DRO, a group-agnostic method, consistently outperforms the rest, scaling effectively to multiple (even intersecting) groups while improving both group-level and overall performance metrics.

📎Code link, Paper here

Context

Recommender systems are among the most widespread applications of machine learning, personalizing user experiences on platforms such as:

Amazon shopping
YouTube, TikTok, Instagram feed
Netflix movie recommendations…

These systems offer significant benefits. By optimizing for metrics like watch time, items added to cart, and other measures of average-case user engagement, they not only enhance the user experience but also boost platform revenue.

However, the key phrase here is average-case user metrics. More often than not, data or algorithmic biases can cause disparities in these metrics across different user groups.

Groups metrics

As a thought experiment, imagine we train a movie recommender on a large dataset of historical user interactions. After deployment, we observe a sharp drop in watch-time among a subset of users. It turns out these users are primarily in the 50+ age group. In the fairness literature, features like age and sex are referred to as protected groups.

Now suppose we address this issue and perform group-aware training for two groups: <50 and 50+ age users. After redeployment, we notice a different problem—users with low engagement (i.e., few interactions on the platform) are now seeing a drop in watch-time. These types of user segments are referred to as engagement-based groups.

It becomes clear that this kind of ad-hoc, group based training does not scale.

📌

Group based training is problematic

Intersectionality: Users often belong to multiple groups, making it difficult to assign them to a single category.
Legal constraints: In many cases, using protected attributes (e.g., age, sex) is legally restricted.
Group selection is hard: It is impossible to know apriori (i.e., before training) which user group partition leads to the best performance.

Quick Primer on Sequential Recommendation

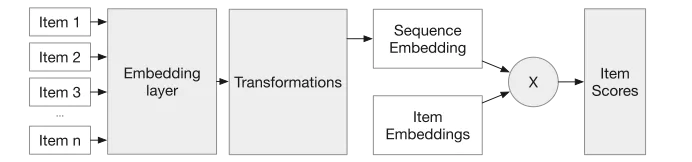
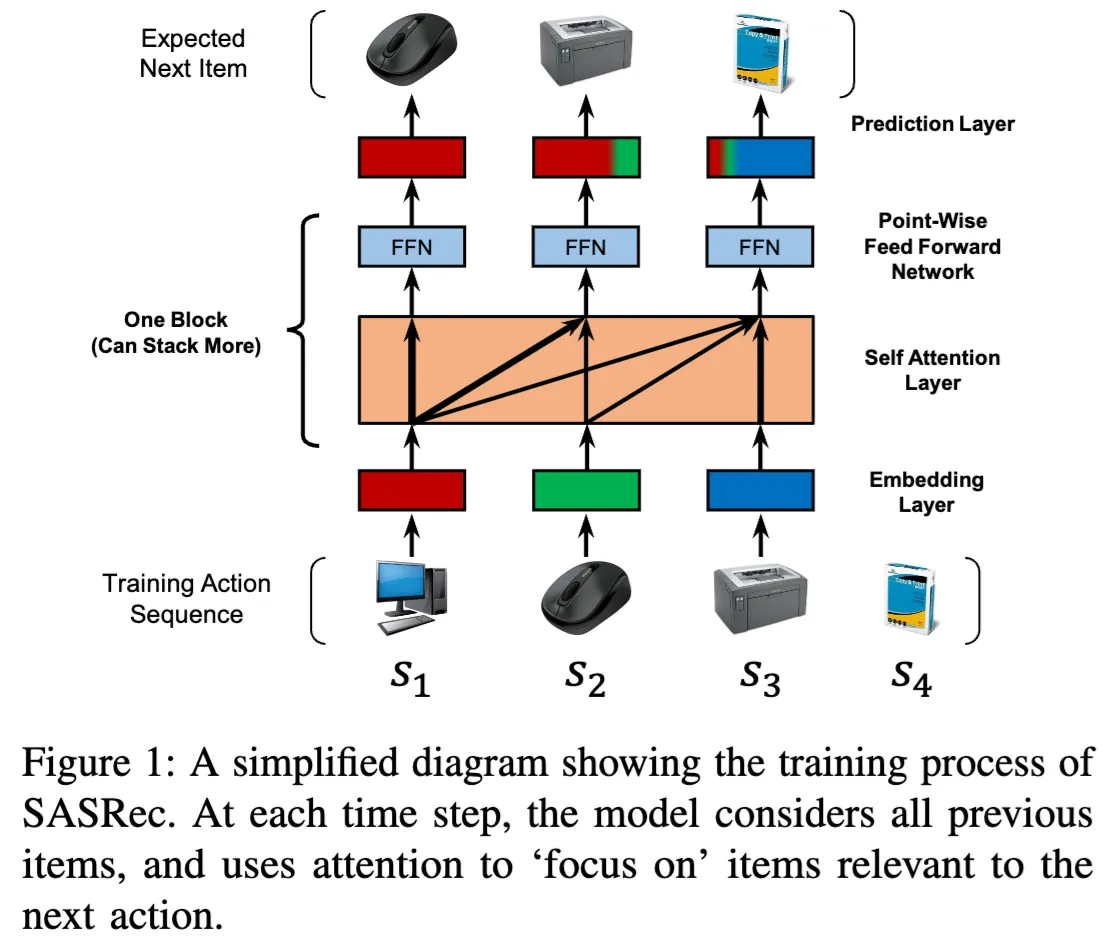
Sequential recommenders predict the next item a user will view based on their previous interactions.

Typical architecture of a sequential recommender, https://arxiv.org/abs/2207.02643 . — Typical architecture of a sequential recommender, https://arxiv.org/abs/2207.02643.

Transformer-based models like SASRec and its variants are great for this task and are widely deployed in practice (MetaTransducers,PinnerFormer).

These models are typically trained with standard training or “Empirical Risk Minimization(ERM)”, which minimizes the average cross entropy loss (across all users sequences) but can sacrifice performance on minority groups.

Self-Attentive Sequential Recommendation https://arxiv.org/pdf/1808.09781

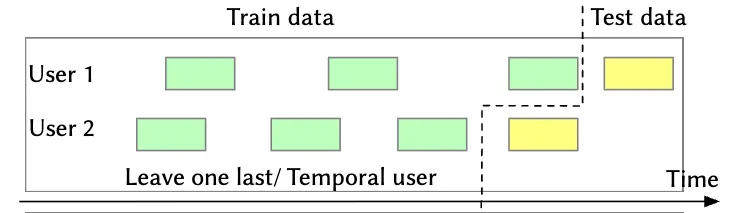
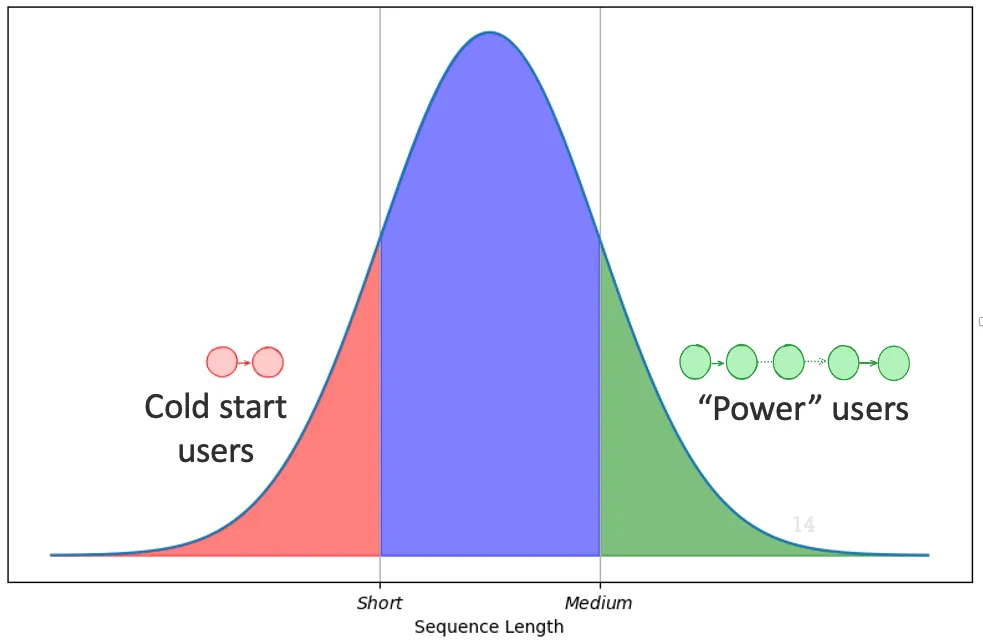
Leave one out (LOO) split

Leave one out split, https://arxiv.org/pdf/2007.13237

The leave one out (LOO) split is a standard approach for training sequential recommender systems. As shown in the figure above, the final item in a user's interaction sequence is held out for testing and all preceding items are used for training.

Note: For hyperparameter tuning, it's common to reserve a small subset of users typically around 5% for validation. For these users, the first $n-2$ items are used for training, the $(n-1)^{th}$ item serves as the validation target item, and the final item is used for testing.

For the remaining 95% of users we use the first $n-1$ items for training and the last item for testing.

Group Fairness

A common approach to group fairness is to equalize true positive rates (recall) across user groups. Ideally, this involves reducing the error rate for disadvantaged groups to match that of advantaged ones. However, many existing algorithms achieve this parity by increasing the error rate for advantaged groups—an undesirable outcome.

Minimax Group Fairness

In contrast, minimax group fairness explicitly aims to minimize the maximum loss for any group. Let $\theta$ represent the model parameters(e.g. weights of the neural network) and let $L_k(\theta)$ denote the loss of the model on users $(x,y)$ belonging to group $G_k$ .

The minimax-optimal model parameters is thus defined as:

\theta_{minmax} = \argmin_\theta \left[\max_k L_k(\theta) \right]\text{ where } L_k = \frac{1}{|G_k|} \sum_{(x,y) \in G_k} Loss(\theta(x),y)

Note that the minimax solution does not guarantee balanced performance across all groups. Instead, it focuses solely on improving the performance of the worst-performing group, even if that results in disparities persisting across groups.

Distributionally Robust Optimization(DRO)

Recall that standard training — or, in fancy learning theory terms, Empirical Risk Minimization (ERM) is defined as minimizing the loss on examples drawn from the training data.

\theta_{ERM} = \argmin_\theta \left[ \mathbb{E}_{(x,y) \sim D_{train}} L(\theta(x),y) \right]

In Distributionally Robust Optimization (DRO), the idea is to construct an uncertainty set around the training distribution, denoted as $\hat{D}_{train}$ , and then solve a minimax problem. The inner maximization is performed over all distributions $\hat{D}_{train}$ that are considered "close" to the training distribution $D_{train}$ .

\theta_{DRO} = \argmin_\theta \left[ \max_{\hat{D}_{train}} \mathbb{E}_{(x,y) \sim \hat{D}_{train}} L(\theta(x),y) \right]

There are different notions of “closeness” of distributions and this leads to different DRO training algorithms.

Existing methods using DRO-Based training in recsys

Wen at al propose GroupDRO(gDRO) and a variant Streaming DRO(sDRO) for a two-tower model. The uncertainty set $\hat{D}_{train}$ is defined as a mixture of user groups. In each batch they maintain a tuple of (weights, losses) for each group and backpropagate $L = \sum_g w_g L_g$ , the weights are updated to give higher weight to the group with larger loss:

w_g^t \propto exp(\eta L_g^t) w_g^{t-1}

If you’re curious about this its related to the exponential weights update for the inner maximization problem, $\eta \in [0,1]$ is the exp-weights learning rate. Note that training with gDRO or sDRO requires group attributes so we face the group based training limitations discussed earlier in this writeup.

CVaR: A group agnostic training method

These challenges with group specific training motivated us to look for a method that is group-agnostic, easily fits into existing training pipelines and has few hyperparameters.

CVaR-DRO[Levy et al] fits all these criteria and you can find my integration for recommendation here.

Loss_{CVaR}^\theta(\alpha) = \max_{q \in \Delta^B} \left\{ \sum_{u=1}^B q_u \cdot l_u^\theta ~ \vert ~ ||q||_\infty \leq \frac{1}{\alpha B} \right\}

The CVaR Loss takes as input the loss for each user $u \in [B]$ in the batch of size $B$ and calculates the loss for the worst $\alpha$ B users. The main idea is that this implicitly identifies a group of users with high loss, without requiring explicit group annotations. Note that $\alpha \in [0,1]$ is a hyperparameter that is tuned based on overall nDCG on validation set.

Experiments

Datasets

RetailRocket an ecommerce session dataset
MovieLens1M a classic movie ratings dataset.

Note that both datasets have timestamps for user-item interactions, and are processed so that each item sequence for a user is sorted chronologically.

Engagement-Based Groups

We consider two types of user groups based on engagement characteristicsShow information for the linked content:

Popularity: Defined as the ratio of popular items in a user's interaction history.
Sequence Length: Defined by the number of items a user has interacted with.

Popularity based groups

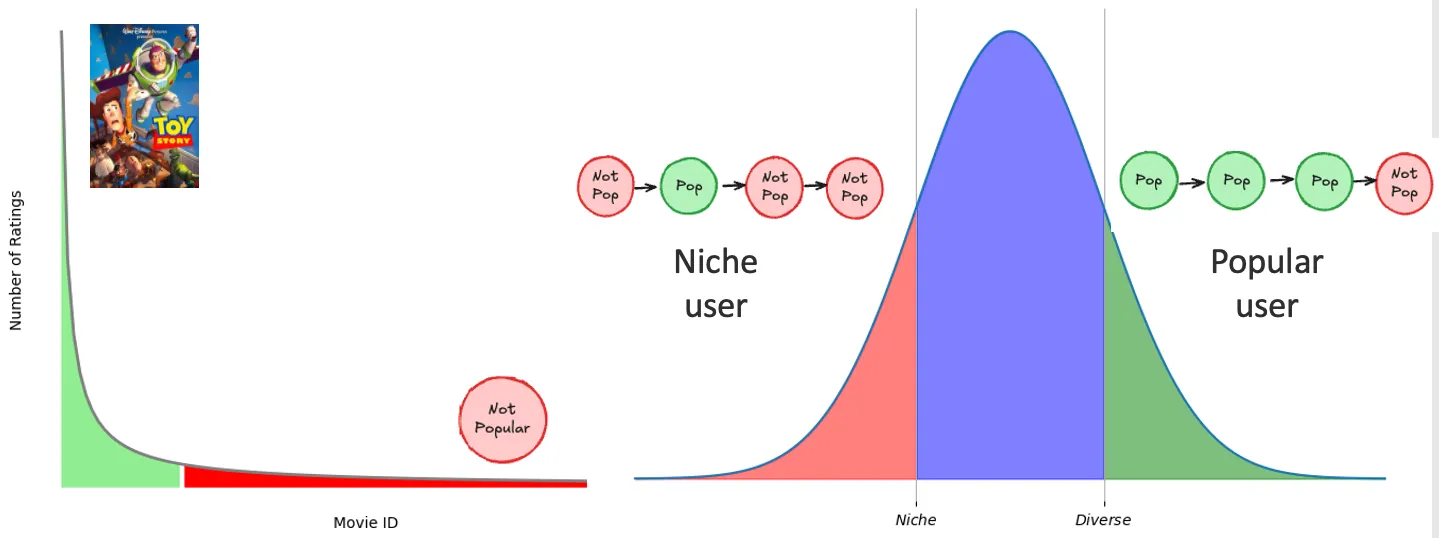
Recommendation quality disparities have been well-documented between niche and mainstream users. For example, music listeners who primarily engage with mainstream content (e.g., Billboard Hot 100) tend to receive significantly better recommendations than those who listen to niche playlists.

Music listeners who listen to a lot mainstream music (e.g. Hot 100) get much better recommendations than those niche playlists https://arxiv.org/pdf/2102.12188

The number of ratings per item follows a long-tail distribution, with a small number of popular items receiving the majority of interactions. Following Wen et al, we label a user as "popular" if they have a high ratio of popular items in their watch history. We divide users into three subgroups—niche, diverse, and popular—depending on which quantile their ratio falls into.

The number of ratings per item follows a long-tail distribution ( left ). Users are categorized based on the ratio of popular items in their history—high ratios are labeled "popular" , and others as "diverse" or "niche" ( right ). — The number of ratings per item follows a long-tail distribution (**left**). Users are categorized based on the ratio of popular items in their history—high ratios are labeled **"popular"**, and others as **"diverse"** or **"niche"** (**right**).

Ablation: Varying Quantiles and Group Sizes $(G_{bal}, G_{2060}, G_{1080})$

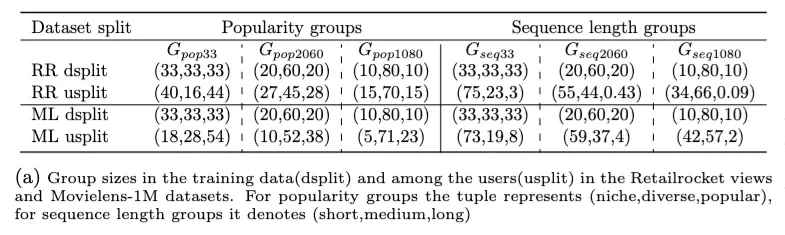
We compare training methods across varying group sizes using three quantile splits: balanced (33% each), semi-balanced (20%, 60%, 20%), and imbalanced (10%, 80%, 10%). For example, in the first cell of Table 1a, if the bottom, middle, and top quantile for the ratio of popular items are 40%, 16%, and 44%, this results in the data having an equal mix of niche, diverse, and popular users.

See Table 1 in our paper for more details https://arxiv.org/pdf/2501.18117

Sequence length groups

Inspired by the cold-start literature—where users with different interaction lengths often receive recommendations of varying quality—we categorize users as short, medium, or long, based on whether their sequence length falls into the bottom, middle, or top quantile.

We consider 3 subgroups for users with short, medium and long interactions

Results

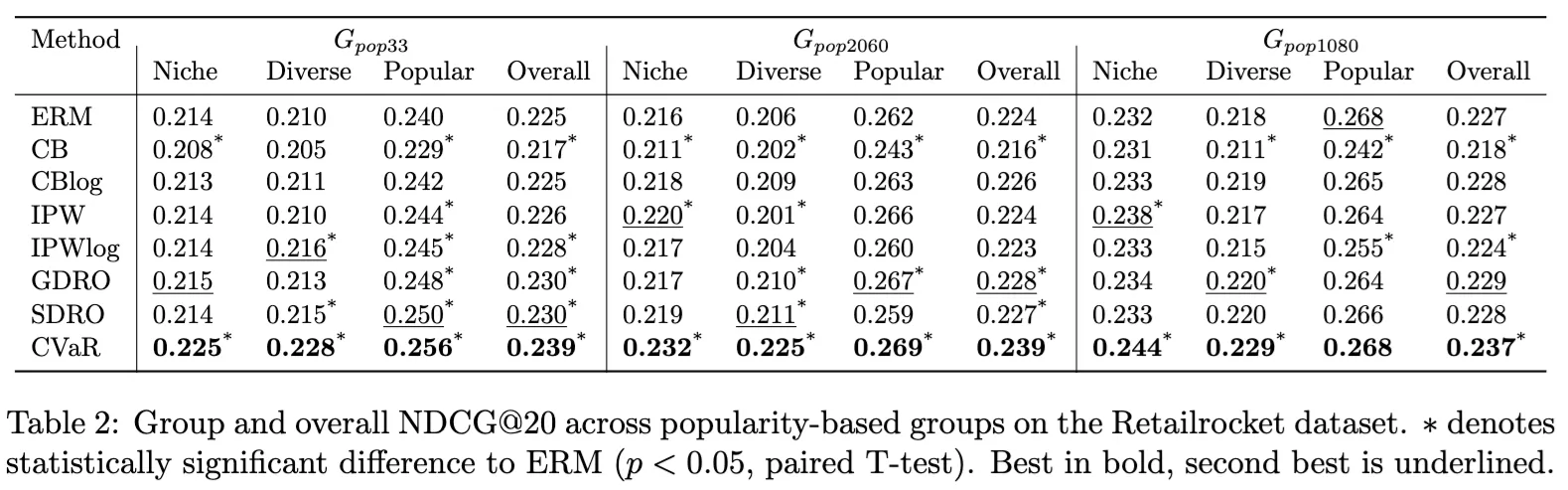
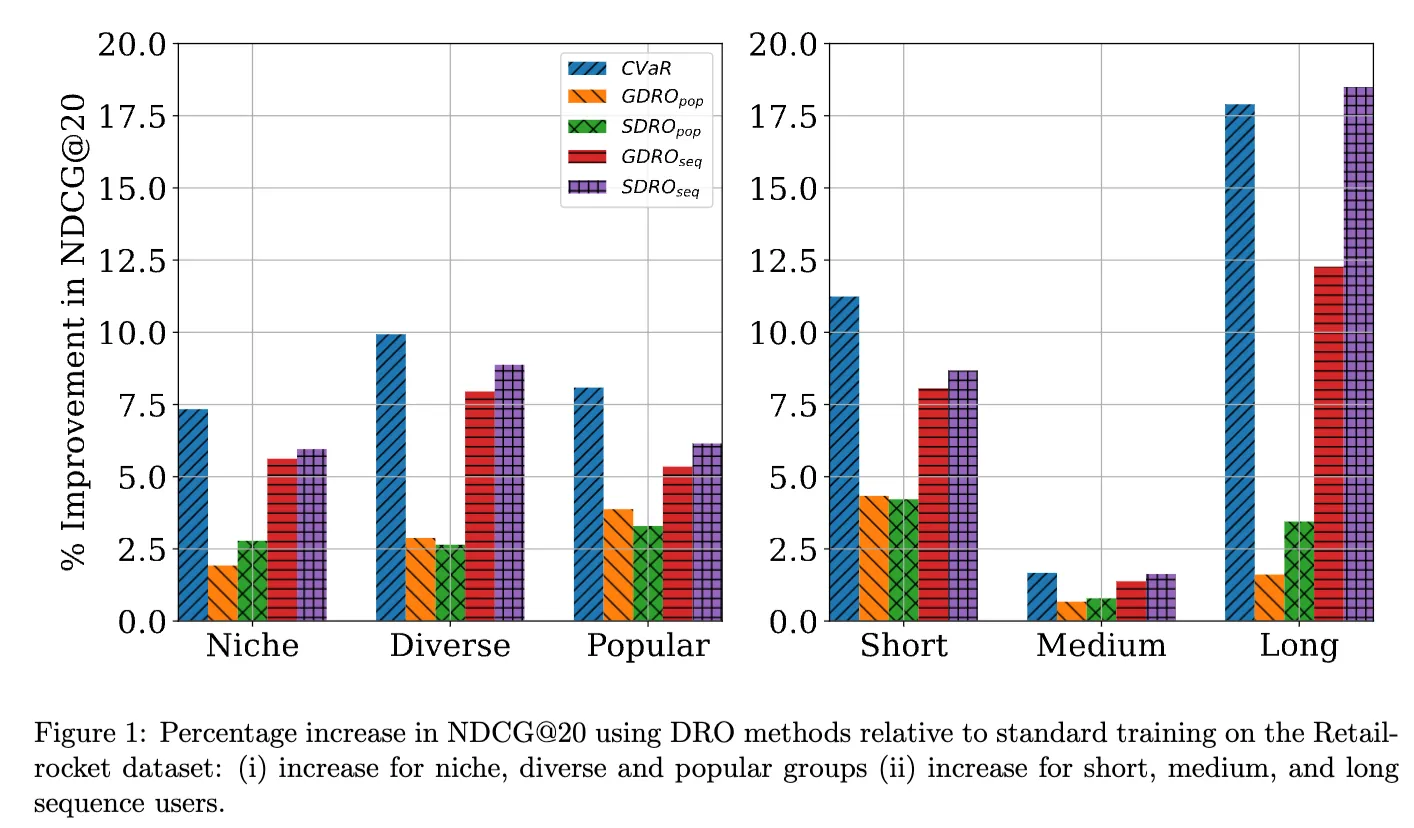
Measuring NDCG@20 for the popularity based groups

CVaR-DRO achieves highest NDCG across all groups and overall highest NDCG
This is true even for the very imbalanced $G_{pop1080}$ group, where the group-dependent methods(GroupDRO, StreamingDRO) struggle to improve on vanilla training (ERM)

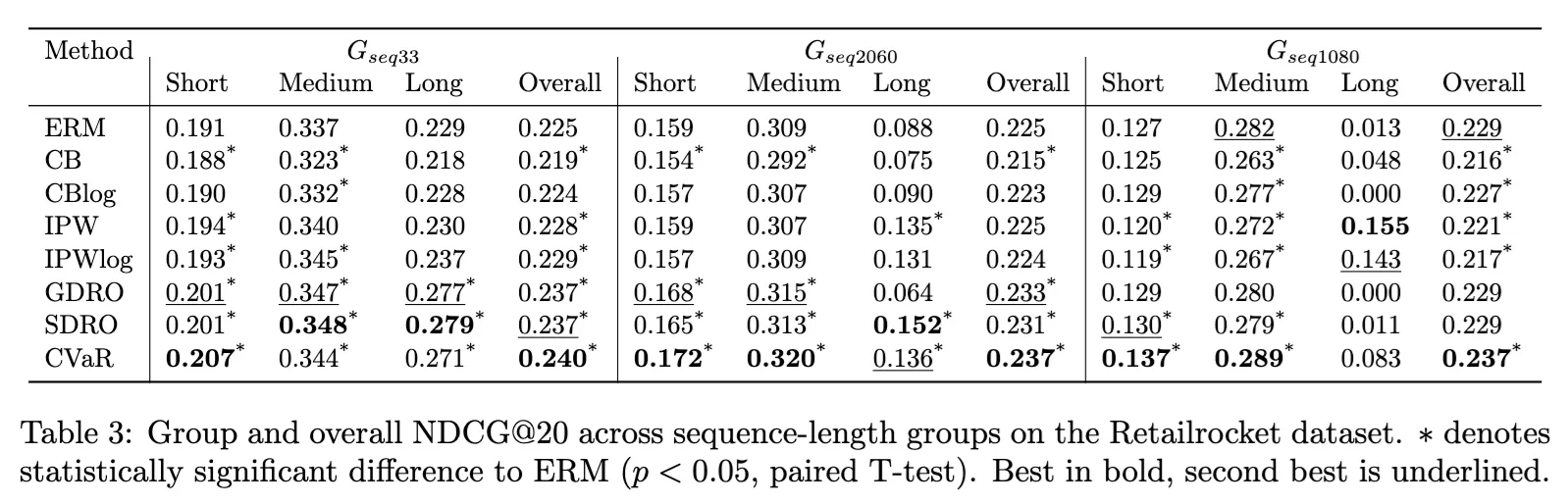
Measuring NDCG@20 for the sequence length groups

CVaR-DRO achieves highest NDCG overall and for 5/9 groups.
Again, CVaR outperforms group-based methods on the very imbalanced group $G_{seq1080}$

Measuring NDCG@20 with intersecting groups

CVaR outperforms group-based methods overall and in 5/6 groups
We observe that training with popularity-based groups is always worse than using sequence based groups $\implies$ group-dependent methods are very sensitive to misspecification, and it’s impossible to know apriori which group is best.

Conclusion

Standard training (ERM) can lead to poor performance for sequential recommendation
Group-based DRO methods (Group DRO, Streaming DRO) help, but face several challenges:
- Require predefined user groups:
  - Performance is very sensitive to group choice, which is often unknown beforehand.
  - May be legally prohibited to use protected attributes (e.g., age, sex).
- Cannot handle intersecting groups.
- Performance can degrade with imbalanced group sizes.
Conditional Value at Risk (CVaR) DRO addresses these issues:
- Does not rely on explicit group definitions.
- Can still significantly improve both group-specific and overall performance metrics.